From the previous learning, we know that energies within an energy system transfer into different forms, but the total energy does not change. Today, we continued to investigate the transference between GPE and kinetic energy by doing the following activity.
Two ramps with different length have been set to an angle to the horizon, one is steeper than the other. Two balls with the same mass have been placed on the top of each ramp, which had the same height. If both balls have been released at the same time, which ball would reach point B first?
The answer was ball 2. This occurred because it took shorter time for ball 2 to completely transfer GPE into kinetic energy. As we know, the kinetic energy of the ball when it hit the table equaled to the GPE it had before releasing. As ball 2 traveled at a steeper angle and shorter distance, it could transfer GPE into kinetic energy within shorter time compare to ball 1.
However, we also learned that the velocity for both ball when they pass point B would be the same because they had the same GPE. This means they had the same kinetic energy, and so they would pass through point B with the same velocity.
Another thing we learned today was the conservation of energy in roller coasters. As the roller coaster traveled down from its starting point, its GPE would equal to its kinetic energy when it reached the bottom of the ramp. However, what would the velocity be when it reached point B in the following diagram if there was no friction?
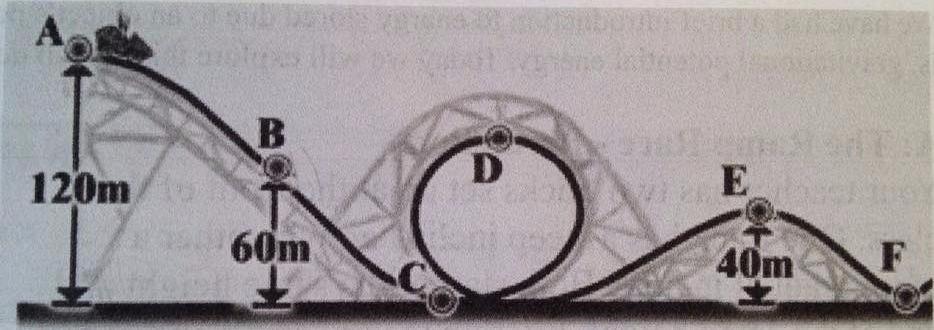
Since we know the total energy does not change no matter what, and the mechanical energy of roller coaster at point B was the sum of kinetic energy and GPE. Thus, we could say GPE at point A equal to GPE + kinetic energy at point B. So we could get the following equation:
mg hA = mg hB +1/2 mv^2
simplify the equation:
g hA = g hB + 1/2 v^2
By plugging in the numbers from the diagram, the question would be solved:
9.8 m/s^2 (120m) = 9.8 m/s^2 (60m) + 1/2 v^2
v^2 = [9.8 m/s^2 (120m) - 9.8 m/s^2 (60m) ] x2
v = 32 m/s